This is a copy of my original post on Kudelski Security’s Research Blog for my archives.

During an internal work project pertaining to automated cryptographic testing, I've discovered that many implementations don't respect standard specifications, especially signature algorithms. Let us take a deeper look into it. We will mostly discuss the DSA and ECDSA algorithms and their respective domains and parameters.

It is important to know that both of those digital signature algorithms were brought to the scene by standards, respectively the NIST FIPS 186, also known as the "Digital Signature Standard" and the ANSI X9.62 (which is paywalled, but a free description is available here). Note that the FIPS 186 in its current 186-4 version also discuss ECDSA. This means that most implementers (hopefully) referred to those documents to add the algorithms to their software.

DSA

Standards always include many recommendations, which are not always followed by the implementer afterwards. For instance, the DSA key parameters are restricted to four different pairs of key lengths $(L, N)$ in the standard: $(1024, 160), (2048, 224), (2048, 256),$ and $(3072, 256)$, while many implementations actually accept keys of any size.

While this may not appear to be a problem, there are other checks an implementation may fail to perform. Let us first study the DSA case. According to FIPS 186-4, the DSA parameters are defined as follows:

• $p$ is a prime modulus, where $2^{L-1} < p < 2^L$, and $L$ is the bit length of $p$.
• $q$ is a prime divisor of $(p - 1)$, where $2^{N-1} < q < 2^N$, and $N$ is the bit length of $q$.
• $g$ is a generator of a subgroup of order q in the multiplicative group of $GF(p)$, such that $1 < g < p$.
• $x$ is the private key that must remain secret; $x$ is a randomly or pseudorandomly generated integer, such that $0 < x < q$.
• $y$ is the public key, where $y = g^x \mod p$.
• $k$ is a secret number that is unique to each message;
• $k$ is a randomly or pseudorandomly generated integer, such that $0 < k < q$.

We call $(p, q, g)$ the domain parameters.

Note that $k$ is usually generated during the signature process and must be kept secret. Now, the standard also specifies both for DSA and ECDSA that the signing operation should go as follows:

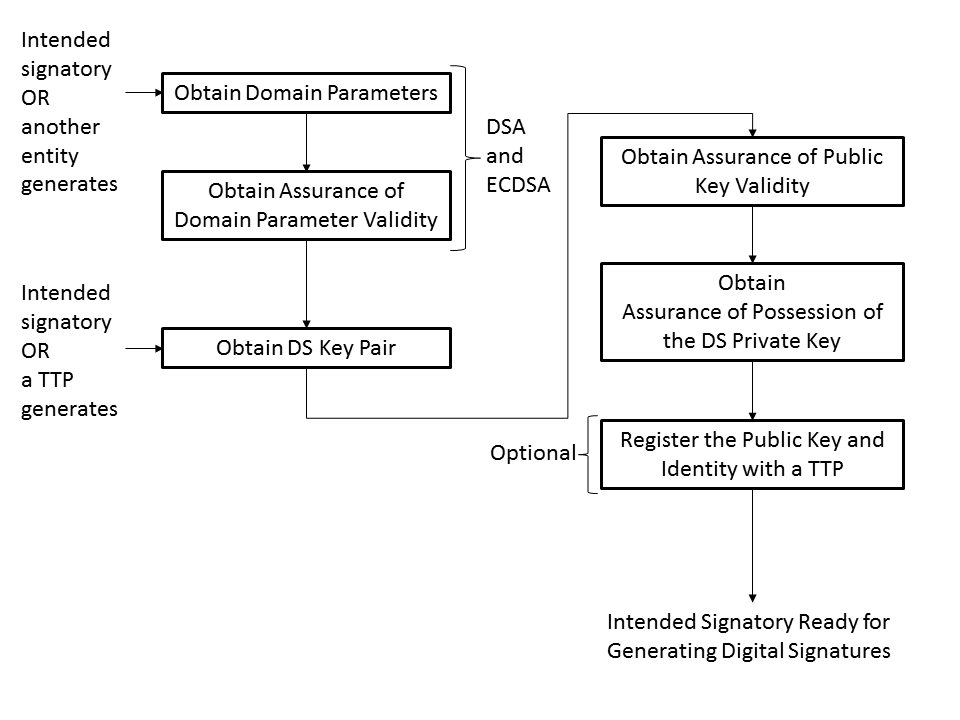
Now, as you can see, "obtain assurance of domain parameter validity" as well as "obtain assurance of public key validity" are both part of the process. And the same holds for verification, which goes as follows:

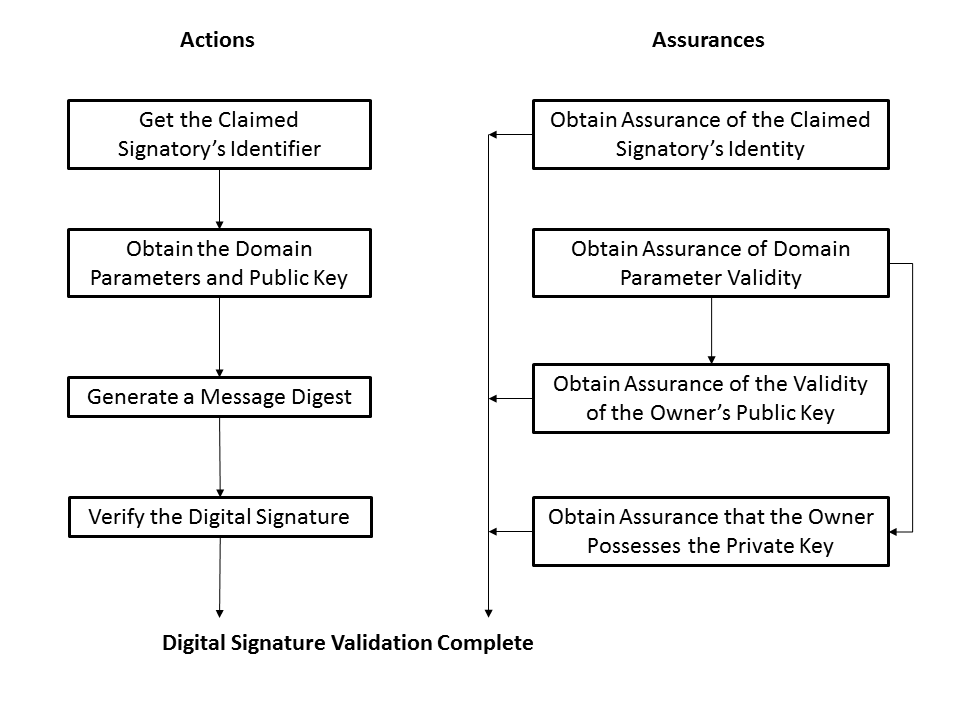
Now, it is interesting that the domain parameters in the signing process may be generated by another entity — that is, potentially by an adversary. For the following, I'll assume that you know how (EC)DSA work. If not, their respective Wikipedia pages (DSA, ECDSA) are enough to get the idea and understand the rest of this article. Let us begin with DSA. The standard states the following regarding signature generation:

The values of $r$ and $s$ shall be checked to determine if $r=0$ or $s = 0$.
If either $r = 0$ or $s = 0$, a new value of $k$ shall be generated, and the signature shall be recalculated. It is extremely unlikely that $r = 0$ or $s = 0$ if signatures are generated properly.

Now, when implementing DSA, most implementations follows the following idea: as long as we end up either with $r$ or $s$ equal to $0$, then we can loop back to generating a new $k$. In Go v1.7.4, for instance it was implemented as follows:

for {
	k := new(big.Int)
	buf := make([]byte, n)
	[...]
	kInv := fermatInverse(k, priv.Q)

	r = new(big.Int).Exp(priv.G, k, priv.P)
	r.Mod(r, priv.Q)

	if r.Sign() == 0 {
		continue
	}

	z := k.SetBytes(hash)

	s = new(big.Int).Mul(priv.X, r)
	[...]
	if s.Sign() != 0 {
		break
	}
}

Now, what would happen to such an implementation if it were to try to compute a signature using $g=0$ as a domain parameter? Then it would cause r = new(big.Int).Exp(priv.G, k, priv.P) to be always equal to $0$, and the branch if r.Sign() == 0 would always be taken, causing an infinite loop, resulting in a potential DoS by CPU exhaustion. A possible workaround, as it can now be found in Go v1.8.0 after our report, would be to limit the loop to a few iterations and checking if we get stuck or not:

var attempts int
for attempts = 10; attempts > 0; attempts-- {
	k := new(big.Int)
	[...]
}
// Only degenerate private keys will require more than a handful of
// attempts.
if attempts == 0 {
	return nil, nil, ErrInvalidPublicKey
}

While this is a simple workaround, actually the best way to ensure such case would not happen is to perform proper domain parameters and key validity checks prior to using any key material to perform DSA, as specified.

If you believe that the infinite loop is not a bug but a feature, then you share the opinion of the OpenSSL team, which did not patch against it:

/*
* Redo if r or s is zero as required by FIPS 186-3: this is very
* unlikely.
*/
if (BN_is_zero(ret->r) || BN_is_zero(ret->s))
	goto redo;

It will fall in an infinite loop if $g=0$, for example.

Now, imagine the following scenario, which is not too far-stretched in my opinion:

• A server and a client are communicating.
• The server ask the client for the domain parameters he would like to use, as the standard seems to allow.
• The client provides maliciously crafted domain parameters, for example with $g=0.$
• The server generate a key pair using those parameters, sends the public key to the client.
• The server uses the private key to perform signature operations.
• The server is vulnerable because he used the invalid domain parameters provided.

This scenario is possible only if the server does not obtain assurance of the domain parameters validity, since otherwise it would have rejected them and would not actually use the malicious input.

There are actually more risks than “just” a DoS here: imagine the client is passing as a generator the value $g=1$, then, if no proper checks are performed the key pair generated at step 4 would be bogus. (Note that in the Go case, the documentation of func GenerateKey states that “the Parameters of the PrivateKey must already be valid”, but no function currently allows to check it. In the OpenSSL case, this is undocumented.)

How bogus is the key pair generated when $g=1$? Well, let us take a look at the way the DSA public and private keys are generated, when given $p, q$ and $g$:

• Choose a secret key $x$ at random, so that $0< x<q$
• Compute the public key $y = g^x \mod p$

So, if $g = 1$, then $y=1^x = 1$. And then the verification process only relies on the fact that $s$ must then be equal to $1$, which is easily crafted.

ECDSA

We also discovered that libraries using the ECDSA algorithm were not always checking whether the points used in its computations were actually on the curve or not. Indeed, ECDSA sports so-called ECDSA parameters, which are an elliptic curve $\mathcal{C}$, a base point $G$, which is a generator of the elliptic curve with a large prime order $n$, that is, such that $n \times G = 0$, where $\times$ denotes the elliptic curve point multiplication by a scalar.

An ECDSA key pair is constituted of a private key integer $d$ and a public key point $Q = d\times G$ on the curve $\mathcal{C}$.

What happens if we provide a base point $G$ that is not on the curve?

Well, then the public key $Q$ may also not be on the curve, and further computations may lead to so-called invalid curve attacks. Such attacks have been extensively studied in the Diffie-Hellman key exchange and other TLS-relevant cases, but the literature is scarce regarding ECDSA. That’s primarily because, just like for DSA, an attacker-provided generator is a somewhat doubtful case. Even then, we would expect that a new private key be generated for that generator. The public key would also show the fact that there is some problem. So basically the practicality of such an invalid curve attack against ECDSA is limited. Vaudenay quickly mentioned the fact that “similar attacks hold for ECDSA”, regarding generator attacks like those we discussed above for DSA in his 2003 article on The Security of DSA and ECDSA.

Nonetheless, as the ECDSA standard states, assurance of the validity of the public and private key material shall be obtained and checking in the EC context whether the different points used belong to the curve may also tamper fault attacks or hardware failures.

Conclusion

In the end, it is important to keep in mind that the standards are there for a reason and involved a lot of reflexion. Even if the basic checks recommended may seem unnecessary, in practice those are the last safeguards against the lack of user awareness. We cannot expect extensive cryptographic knowledge from every developer and libraries should equally support use cases that their own developers did not think of. If you are reading this and are maintaining a software project implementing its own (EC)DSA, please check that you do not miss domain parameters and key validation in your codebase.